TEORI KOMBINATORIAL
Assalamualaikum wr.wb.
Kali ini saya akan membahas materi tentang Teori Kombinational
Teori Kombinatorial merupakan salah satu pokok bahasan Matematika Diskrit yang telah banyak dikembangkan dan diaplikasikan dalam berbagai bidang. Dalam perkembangan Matematika, dapat dilihat bahwa kajian kombinatorial sangat menarik bagi sebagian orang. Salah satu contoh permasalahan yang dapat diselesaikan dengan kombinatorial adalah menghitung banyaknya kombinasi angka nomor polisi mobil, di mana nomor polisi terdiri atas lima angka dan diikuti dua huruf, serta angka pertama bukan nol.
Cara paling sederhana untuk menyelesaikan persolan sejenis adalah dengan mengenumerasi semua kemungkinan jawabannya. Mengenumerasi berarti mencacah atau menghitung satu per satu setiap kemungkinan jawaban. Akan tetapi enumerasi masih mungkin dilakukan jika jumlah objek sedikit, sedangkan untuk persoalan di atas, cara enumerasi jelas tidak efisien. Misalnya untuk menjawab persoalan di atas, apabila kita melakukan enumerasi, maka kemungkinan jawabannya adalah sebagai berikut:
12345AB
12345AC
12345BC
…
34567MT
34567ML
…
dan seterusnya…
Sangatlah mungkin bahwa kita sudah lelah sebelum proses enumerasi selesai dilakukan. Di sinilah peran kombinatorial, yang merupakan “seni berhitung”, menyelesaikan persoalan semacam ini dengan cepat. Demikian juga dalam permainan Poker. Peluang seorang pemain untuk mendapatkan kombinasi lima kartu yang ada dapat dihitung dengan cepat dengan menggunakan kombinatorial. Pada dasarnya, Poker adalah permainan berdasarkan keberuntungan. Oleh karena itu, pemain yang mendapat kartu yang paling sulit didapatkan (artinya, memiliki peluang kemunculan sangat kecil) adalah pemenangnya. Dengan demikian, urutan bagus atau tidaknya suatu kartu dapat dihitung secara matematis dengan menggunakan kombinatorial dan teori peluang.
Teori Kombinatorial
Kombinatorial adalah cabang matematika untuk menghitung jumlah penyusunan objek-objek tanpa harus mengenumerasi semua kemungkinan susunannya.
Kaidah Dasar Menghitung
1. Kaidah Perkalian (rule of product)
Misalkan percobaan 1 mempunyai p hasil percobaan, dan percobaan 2 mempunyai q hasil, maka bila percobaan 1 dan percobaan 2 dilakukan akan terdapat p × q hasil percobaan.
2. Kaidah Penjumlahan (rule of sum)
Misalkan percobaan 1 mempunyai p hasil percobaan, dan percobaan 2 mempunyai q hasil, maka bila percobaan 1 atau percobaan 2 dilakukan (hanya salah satu percobaan saja yang
dilakukan) akan terdapat p + q hasil percobaan.
Permutasi
Permutasi adalah jumlah urutan yang berbeda dari pengaturan objek-objek. Permutasi merupakan bentuk khusus aplikasi kaidah perkalian.
Misalkan jumlah objek adalah n, maka
Urutan pertama dipilih dari n objek,
urutan kedua dipilih dari (n – 1) objek,
urutan kedua dipilih dari (n – 2) objek,
…
urutan terakhir dipilih dari 1 objek yang tersisa.
Menurut kaidah perkalian, permutasi dari n objek adalah n(n – 1)(n – 2) … (2)(1) = n!
Rumus permutasi-r (jumlah susunan berbeda dari pemilihan r objek yang diambil dari n objek), dilambangkan dengan P(n,r):

Kombinasi
Bentuk khusus dari permutasi adalah kombinasi. Jika pada permutasi urutan kemunculan diperhitungkan, maka pada kombinasi, urutan kemunculan diabaikan.
Rumus kombinasi-r (jumlah pemilihan yang tidak terurut r elemen yang diambil dari n buah elemen), dilambangkan dengan C(n,r) atau ( n r ) .
Interpretasi Kombinasi
1. C(n, r) = banyaknya himpunan bagian yang terdiri atas r elemen yang dapat dibentuk dari
himpunan dengan n elemen.
2. C(n, r) = cara memilih r buah elemen dari n elemen yang ada, tetapi urutan elemen di dalam
susunan hasil pemilihan tidak penting.
Permutasi dan Kombinasi Bentuk Umum
Misalkan terdapat n buah bola yang tidak seluruhnya berbeda warna (ada beberapa bola berwarna sama – indistinguishable).
n1 bola di antaranya berwarna 1,
n2 bola di antaranya berwarna 2,
…
nk bola di antaranya berwarna k,
dan n1 + n2 + … + nk = n.
Berapa jumlah cara pengaturan n buah bola ke dalam kotak-kotak tersebut (tiap kotak maksimal 1 buah bola)?
Penyelesaian:
Jika n buah bola itu kita anggap berbeda semuanya, maka jumlah cara pengaturan n buah bola ke dalam n buah kotak adalah P(n, n) = n!
Dari pengaturan n buah bola itu,
Terdapat n1! cara memasukkan bola berwarna 1,
terdapat n2! cara memasukkan bola berwarna 2,
…
terdapat nk! cara memasukkan bola berwarna k.
Permutasi n buah bola yang mana n1 di antaranya berwarna 1, n2 bola berwarna 2, …, nk bola berwarna k adalah
Cara penyelesaian lain:
Terdapat C(n, n1) cara untuk menempatkan n1 buah bola yang berwarna 1,
terdapat C(n – n1, n2) cara untuk menempatkan n1buah bola yang berwarna 2,
terdapat C(n – n1 – n2, n3) cara untuk menempatkan n1 buah bola yang berwarna 3,
…
terdapat C(n – n1 – n2 – … – nk-1, nk) cara untuk menempatkan nk buah bola yang berwarna k.
Jumlah cara pengaturan seluruh bola ke dalam kotak adalah
Kesimpulan:
Kombinasi dengan Pengulangan
Misalkan terdapat r buah bola yang semua warnanya sama dan terdapat n buah kotak, serta ketentuan sebagai berikut:
1. Masing-masing kotak hanya boleh diisi paling banyak satu buah bola.
Jumlah cara memasukkan bola adalah C(n, r).
2. Masing-masing kotak boleh diisi lebih dari satu buah bola (tidak ada pembatasan jumlah bola).
Jumlah cara memasukkan bola adalah
Teori Peluang
Kombinatorial dan teori peluang (probability) berkaitan sangat erat. Teori peluang banyak menggunakan konsep-konsep dalam kombinatorial. Sebenarnya kedua bidang ini lahir dari arena judi (gambling games) – salah satu kasusnya adalah menghitung peluang munculnya nomor lotre tertentu. Meskipun demikian, aplikasi kombinatorial dan teori peluang saat ini telah meluas ke berbagai bidang ilmu lain maupun dalam kehidupan nyata seperti ilmu statistika, fisika, ekonomi, biologi, dan berbagai bidang ilmu lainnya.
Terminologi Dasar
Ruang Contoh (sample space)
Ruang Contoh dari suatu percobaan adalah himpunan semua kemungkinan hasil percobaan
yang bersangkutan.
Titik Contoh (sample point)
Titik Contoh adalah setiap hasil percobaan di dalam ruang contoh. Hasil-hasil percobaan tersebut bersifat saling terpisah (mutually exclusive) karena dari seluruh ruang contoh, hanya satu titik contoh yang muncul.
Misalnya pada percobaan melempar dadu, hasil percobaan yang muncul hanya salah satu dari 6 muka dadu, tidak mungkin muncul dua muka atau lebih, atau tidak mungkin salah satu dari enam muka dadu tidak ada yang muncul.
Ruang Contoh Diskrit (discrete sample space)
Ruang Contoh Diskrit adalah ruang contoh yang jumlah anggotanya terbatas. Misalkan ruang contoh dilambangkan dengan S dan titik-titik contohnya dilambangkan dengan x1, x2, …, maka
S = { x1, x2, …, xi, … }
Menyatakan ruang contoh S yang terdiri atas titik-titik contoh x1, x2, …, xi, dan seterusnya.
Peluang Diskrit
Peluang Diskrit adalah peluang terjadinya sebuah titik contoh, dan disimbolkan dengan p(xi).
Sifat-sifat peluang diskrit adalah sebagai berikut:
1. 0 ≤ p(xi) ≤ 1, yaitu nilai peluang tidak negatif dan selalu lebih kecil atau sama dengan 1. 2.
Kejadian (event)
Kejadian –disimbolkan dengan E– adalah himpunan bagian dari ruang contoh. Misalnya pada percobaan melempar dadu, kejadian munculnya angka ganjil adalah E = {1,3,5}, kejadian munculnya angka 1 adalah E = {1}.
Kejadian yang hanya mengandung satu titik contoh disebut kejadian sederhana (simple event), sedangkan kejadian yang mengandung lebih dari satu titik contoh disebut kejadian majemuk (compound event).
Peluang Kejadian
Peluang Kejadian E di dalam ruang contoh S dapat diartikan sebagai jumlah peluang semua titik contoh di dalam E. Jadi, kita dapat menuliskan bahwa
Logika Permainan sudoku
Sudoku merupakan permainan angka yang berasal dari Jepang. Permainan ini menggunakan kotak 9x9 yang di dalamnya sudah terdapat beberapa angka petunjuk, dan kita diminta untuk melengkapi angka-angka tersebut dengan aturan, tidak ada angka yang sama pada satu baris, satu kolom, atau satu kotak bagian 3x3 yang ditandai garis tebal. Karena semua aturan itu, dalam permainan Sudoku pasti kemunculan setiap angka tepat 9 kali, dari angka yang sudah ada dari awal permainan ditambah dengan angka yang dimasukkan pemain. Permainan ini dapat dilakukan sendirian ataupun bekerja sama dengan orang lain.
Permainan ini tergolong mudah untuk dimengerti semua umur. Semakin cepat anda dapat menyelesaikan suatu permainan Sudoku tanpa trial and error, berarti semakin baik kemampuan logika anda. Tentunya itu juga tergantung tingkat kesulitan permainan Sudoku yang dimainkan, karena kombinasi dari angka pada soal Sudoku menimbulkan kombinasi penyelesaian tersendiri. Dalam makalah ini logika untuk bermain Sudoku akan dibahas. Walaupun ada banyak cara yang dibahas di makalah ini, bukan berarti metode penyelesaian Sudoku hanya itu. Penyelesaian Sudoku masih sangat biasa dikembangkan.
Logika
Logika merupakan dasar dari semua proses penalaran. Dengan logika, kita tahu apa yang benar, apa yang salah, dan apa yang masih tergantung pada variabel lain. Tanpa logika, kita tidak dapat melakukan proses problem solving, oleh karena itu logika merupakan kemampuan yang sangat dasar dalam kehidupan terutama bagi para saintis dan insinyur yang memerlukan proses berpikir sistematis. Sudoku sebagai permainan yang memerlukan pemikiran sistematis tentunya membutuhkan logika. Oleh karena itu, pada makalah ini akan dibahas logika bermain Sudoku yang sering kali tidak terpikirkan orang banyak.
Metode
Notasi
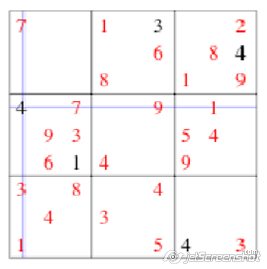
Untuk mempermudah penjelasan pada makalah ini, kita membutuhkan notasi dan catatan kecil. Catatan kecil yang dimaksudkan adalah penulisan kemungkinan angka pada suatu kotak. Oleh karena itu, kita akan melihat terkadang terdapat lebih dari satu angka pada suatu kotak di gambar
contoh. Itu akan mempermudah kita untuk memperkirakan apa isi suatu kotak.
Untuk notasi, kita menggunakan notasi seperti berikut.
U : himpunan universe, {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Kij : menunjukkan kotak pada baris i, kolom j.
Pij : menunjukkan himpunan kemungkinan angka pada baris i, kolom j.
Bi : menunjukkan himpunan angka yang telah muncul pada baris i.
BiX : menunjukkan himpunan kotak pada baris i yang mungkin diisi oleh angka X.
Klj : menunjukkan himpunan angka yang telah muncul pada kolom j.
KljX : menunjukkan himpunan kotak pada kolom j yang mungkin diisi oleh angka X.
Ktx : menunjukkan himpunan angka yang telah muncul pada kotak x.
Nama dari setiap kotak adalah sebagai berikut.
KtxX : menunjukkan himpunan kotak pada kotak x yang mungkin diisi oleh angka X.
Cara menyelesaikan sudoku
Himpunan kemungkinan angka beranggota tunggal.
Dalam Sudoku, setiap satu kotak kecil hanya dapat diisi oleh satu angka. Kemungkinan angka yang dapat ditetapkan pada satu kotak ditentukan oleh angka-angka yang sudah muncul dari sebelumnya pada satu baris yang sama, kolom yang sama, dan subkotak yang sama.
Semakin variatif angka di sekitarnya, semakin sedikit kemungkinan angka pada kotak tersebut. Penentuan itu dilakukan dengan mencari selisih himpunan kemungkinan angka pada satu kotak dengan himpunan angka-angka yang sudah muncul pada satu baris yang sama, kolom
yang sama, dan subkotak yang sama. Karena pada setiap kotak kecil hanya boleh ada tepat satu angka, maka dapat dipastikan jika kemungkinan angka pada kotak tersebut hanya satu, maka angka satu-satunya anggota himpunan itu lah yang tepat untuk diisikan pada kotak tersebut.
Karena dan merupakan himpunan beranggota tunggal, maka pasti berisi angka 3.
b. Dua himpunan beranggota sama.
Untuk menjelaskan masalah himpunan-himpunan beranggota sama dengan mudah, pertama-tama kita akan membahas kasus dengan hanya dua himpunan.
Kita dapat melihat catatan kecil berwarna biru pada K49, K59, dan K69 yang semua kotak itu terdapat pada subkotak yang sama dan kolom yang sama.
b. Dua himpunan beranggota sama.
Untuk menjelaskan masalah himpunan-himpunan beranggota sama dengan mudah, pertama-tama kita akan membahas kasus dengan hanya dua himpunan.
Jika kita lihat pada gambar di atas, sesuai catatan kecil berwarna biru kita dapat mengetahui bahwa P47 dan P68 sama-sama {2, 3}, sama-sama hanya berisi dua kemungkinan (perhitungannya akan dijelaskan pada bagian kemungkinan-kemungkinan tersembunyi).
Istimewanya kesamaan himpunan ini adalah, jika P47 dimasukkan angka 2 atau 3, maka P68 menjadi himpunan beranggota tunggal sehingga bisa langsung diisi. Begitu juga jika P68 diisi, maka P47 menjadi himpunan beranggota tunggal. Dengan ini, walau kita tidak dapat langsung menentukan isi dari P47 dan P68, kita dapat menyimpulkan bahwa angka 2 dan 3 tidak mungkin ditempatkan di kotak lain pada KtA.
Perlu diperhatikan, karena kita hanya memperkirakan angka-angka apa saja yang mengisi dua buah kotak, maka teorema ini hanya berlaku untuk dua kemungkinan angka. Jika ada dua kotak yang memiliki kemungkinan angka sama tapi lebih dari dua kemungkinan angka, teorema ini tidak dapat digunakan.
Selain itu, kedua kotak berhimpunan sama itu harus terletak pada subkotak, baris, atau kolom yang sama.
Himpunan kemungkinan yang terkunci.
Mengembangkan materi dari bagian dua himpunan yang sama, sebenarnya terdapat teorema yang lebih luas dari teorema yang dinyatakan sebelumnya. Jika terdapat beberapa kotak pada subkotak, baris, atau kolom yang sama yang memiliki kemungkinan angka yang ketika digabung jumlah kemungkinannya sama dengan jumlah kotak yang dibicarakan maka angka-angka tersebut pasti ada pada kotak tersebut. Jika jumlah kemungkinan angka hasil penggabungan kurang dari jumlah kotak yang dibicarakan, maka pasti terjadi kesalahan dalam pengisian Sudoku.
Hal ini mempermudah penentuan isi dari kotak yang lain walau kita tidak bisa langsung mengisi kotak-kotak tersebut. Jika kotak-kotak itu muncul pada subkotak yang sama, maka hal ini mempermudah penentuan isi kotak kosong lain pada subkotak tersebut. Jika kotak-kotak itu muncul pada baris yang sama, maka hal ini mempermudah penentuan isi kotak kosong lain pada baris tersebut. Begitu juga jika kotak-kotak itu muncul pada kolom yang sama, maka hal ini mempermudah penentuan isi kotak kosong lain pada kolom tersebut. Untuk ilustrasi kita dapat melihat contoh berikut.
Karena gabungan dari P49, P59, dan P69 menghasilkan himpunan kemungkinan angka yang jumlahnya sama dengan jumlah kotak yang dibicarakan, maka angka 6, 7, dan 8 pada kolom 9 dan subkotak F hanya dapat mengisi. Ini mempermudah penentuan di subkotak F dan kolom 9 sekaligus.
Teorema ini sangat berguna dalam memainkan Sudoku dengan level kesulitan tinggi. Walaupun begitu, teorema ini hanya efektif untuk dua dan tiga kotak. Selebihnya jarang muncul.
Himpunan posisi beranggota tunggal.
Yang akan kita bicarakan mirip dengan yang dinyatakan di bagian himpunan beranggota tunggal. Bedanya, di bagian ini himpunan yang beranggota tunggal adalah himpunan posisi. Misal pada subkotak belum terdapat angka 9 dan hanya ada satu kotak yang mungkin diisi angka 9. Kotak tersebut otomatis harus diisi angka 9 karena subkotak tersebut harus memiliki angka 9
di dalamnya. Contoh :
Sebelumnya pada KtD tidak terdapat angka 1.
Karena kita melihat pada K91 dan K48 terdapat angka 1, maka tentu saja KtD1 menjadi tereduksi.
Karena sekarang hanya berisi , maka angka 1 sudah pasti harus ditempatkan di. Hal ini tidak selalu jelas terlihat pada Sudoku dengan level sangat tinggi. Terkadang kita perlu menguraikan
satu per satu kemungkinan angka pada suatu baris, kolom, atau subkotak untuk menemukannya.
Kemungkinan-kemungkinan tersembunyi.
Inti dari bagian ini seperti pada bagian himpunan posisi beranggota tunggal. Bedanya, di bagian ini kita membicarakan lebih dari satu himpunan, himpunannya berisi lebih dari satu dengan jumlah yang tepat sama dengan jumlah himpunan yang dibicarakan, dan isi himpunannya sama. Tentu saja himpunan-himpunan tersebut harus berletak di baris, kolom, atau subkotak yang sama.
Pada gambar di atas kemungkinan angka pada tiap kotak di KtF telah dihitung dan ditulis dengan catatan kecil biru. Jika diperhatikan KtF2 dan KtF3 sama dengan {K47, K68}. Oleh karena itu, P47 dan P68 dapat disederhanakan menjadi {2, 3}. Untuk perhitungan yang lebih sederhana, kita dapat melihat sekilas bahwa angka 2 dan 3 pada kolom 9 menyebabkan kolom 9 di subkotak F tidak bisa diisi dengan angka 2 dan 3. Sisa kotak yang dapat diisi oleh 2 dan 3 di subkotak F ada 2. Otomatis kotak-kotak tersebut hanya bisa diisi angka 3 dan 2 karena kedua angka tersebut harus mendapatkan tempat. Berikut ini persamaannya.
Baris sisa
Perhatikan gambar di atas. Pada KtD dan KtE telah dibuat catatan tempat yang mungkin diisi dengan angka 8.
Tempat-tempat tersebut memiliki satu kesamaan penting, yaitu, sama-sama hanya terletak di baris ke-5 dan ke-6, berbeda dengan KtF yang memberikan kemungkinan penempatan angka 8 di baris 4, 5, dan 6.
Logika untuk bagian ini, jika pada KtD angka 8 diletakkan pada baris ke-6, maka pada KtE angka 8 harus ditempatkan di baris ke-5. Karena baris ke-6 dan ke-5 sudah memiliki angka 8, maka pada KtF harus menempatkan angka 8 di baris ke-4.
Jika pada KtD angka 8 diletakkan pada baris ke-5, maka pada KtE angka 8 harus ditempatkan di baris ke-6. Karena baris ke-6 dan ke-5 sudah memiliki angka 8, maka pada KtF harus menempatkan angka 8 di baris ke-4.
Pada logika yang berbeda yang dibahas di atas, kita mendapat hasil yang sama, yaitu pada KtF angka 8 harus ditempatkan di baris ke-4, sehingga satu-satunya kotak yang dapat diisi oleh angka 8 adalah K49.
Pengiris transparan
Untuk dapat menyelesaikan Sudoku dengan baik, kita harus dapat melihat pengaruh sesuatu yang baru kemungkinan dengan baik. Kesalahan kebanyakan orang dalam mengerjakan Sudoku biasanya adalah hanya memanfaatkan pengaruh dari data yang terlihat. Prinsip dari pengiris transparan adalah jika KtxX hanya terdapat pada satu kolom atau baris yang sama, maka X pada kolom atau baris tersebut hanya boleh ada pada subkotak x.
Dari gambar di atas dapat dilihat angka 5 di subkotak F mengiris tempat-tempat yang mungkin diisi angka 5 di subkotak C. Dari situ ternyata tinggal dua tempat yang dapat diisi, ditandai dengan catatan kecil biru, dan itu sekolom. Karena subkotak C harus memiliki angka 5 dan mau tidak mau angka 5 tersebut harus ditempatkan di kolom 8, maka di baris 8 di subkotak I tidak dapat diisi angka 5.Dari gambar di atas dapat dilihat angka 5 di subkotak F mengiris tempat-tempat yang mungkin diisi angka 5 di subkotak C. Dari situ ternyata tinggal dua tempat yang dapat diisi, ditandai dengan catatan kecil biru, dan itu sekolom. Karena subkotak C harus memiliki angka 5 dan mau tidak mau angka 5 tersebut harus ditempatkan di kolom 8, maka di baris 8 di subkotak I tidak dapat diisi angka 5.
Percobaan binomial
Percobaan Binomial merupakan suatu percobaan yang memenuhi empat syarat berikut:Terdapat n kali percobaan.
Masing-masing percobaan hanya dapat menghasilkan dua kemungkinan, atau hasil yang diperoleh dapat disederhanakan menjadi dua kemungkinan. Hasil yang diperoleh tersebut dapat dianggap sebagai hasil yang sukses atau gagal.
Hasil dari masing-masing percobaan haruslah saling bebas.
Peluang untuk sukses harus sama untuk setiap percobaan.
Suatu percobaan binomial dan hasilnya memberikan distribusi peluang khusus yang disebut sebagai distribusi binomial.
Hasil-hasil percobaan binomial dan peluang yang bersesuaian dari hasil tersebut dinamakan distribusi binomial.
Dalam percobaan binomial, hasil-hasilnya seringkali diklasifikasikan sebagai hasil yang sukses atau gagal. Sebagai contoh, jawaban benar suatu pertanyaan pilihan ganda dapat diklasifikasikan sebagai hasil yang sukses, sehingga pilihan jawaban lainnya merupakan jawaban yang salah dan diklasifikasikan sebagai hasil yang gagal. Notasi-notasi yang umumnya digunakan dalam percobaan binomial dan distribusi binomial adalah sebagai berikut.
Notasi Keterangan
P(S) Simbol untuk peluang sukses.
P(F) Simbol untuk peluang gagal.
p Peluang sukes.
q Peluang gagal.
P(S) = p dan P(F) = 1 – p = q
n Banyaknya percobaan
X Banyaknya sukses dalam n kali percobaan
Perhatikan bahwa 0 ≤ X ≤ n dan X = 0, 1, 2, 3, …, n.
Peluang sukses dalam percobaan binomial dapat dihitung dengan menggunakan rumus berikut.
Rumus Peluang Binomial
Dalam suatu percobaan binomial, peluang untuk mendapatkan tepat X sukses dalam n percobaan adalah
Untuk mengetahui bagaimana ilustrasi dari rumus peluang binomial tersebut bermula, perhatikan Contoh 1 berikut.
Contoh 1: Melempar Koin
Suatu koin dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka.
Pembahasan Permasalahan ini dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari pelemparan satu koin sebanyak tiga kali adalah
S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}
Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua angka adalah 3/8 atau 0,375.
Dengan melihat kembali Contoh 1 dari sudut pandang percobaan binomial, maka contoh tersebut memenuhi keempat kriteria percobaan binomial.
Terdapat tiga kali percobaan.
Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.
Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-nilai tersebut ke dalam rumus, kita mendapatkan
Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang sampel.
Contoh 1 tersebut juga dapat digunakan untuk menjelaskan rumus peluang binomial. Pertama, perhatikan bahwa terdapat tiga cara untuk mendapatkan tepat dua angka dan satu gambar dari delapan kemungkinan. Ketiga cara tersebut adalah AAG, AGA, dan GAA. Sehingga, dalam kasus ini banyaknya cara kita mendapatkan dua angka dari pelemparan koin sebanyak tiga kali adalah 3C2, atau 3. Secara umum, banyak cara untuk mendapatkan X sukses dari n percobaan tanpa memperhitungkan urutannya adalah
Ini merupakan bagian pertama rumus binomial. (Beberapa kalkulator dapat digunakan untuk menghitung kombinasi tersebut).
Selanjutnya, masing-masing sukses memiliki peluang ½ dan muncul sebanyak dua kali. Demikian juga masing-masing gagal memiliki peluang ½ dan muncul sekali. Sehingga akan memberikan,
pada rumus binomial. Sehingga apabila masing-masing percobaan sukses sukses memiliki peluang p dan muncul X kali serta peluang gagalnya adalah q dan muncul n – X kali, maka dengan menuliskan peluang percobaan sukses kita akan mendapatkan rumus binomial.
Mungkin Itu Saja yang bisa saya sampaikan.
Kurang lebihnya saya mohon maaf.
Wassalamualaikum wr.wb.